Median of Two Sorted Arrays Java Program - The Coding Shala

Home >> Interview Questions >> Median of two sorted arrays

Median of Two Sorted Arrays Java Program

There are two sorted arrays nums1 and nums2 of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.



Example 1:

nums1 = [1,2]

nums2 = [3,4]

The median is 2.5.



Example 2

nums1 = [3]

nums2 = [-1, -2]

The median is -2.

Median of Two Sorted Arrays Java Program


Before solving this we'll see what is median and how to find it. So basically a median is the value present at the center of a sorted array. Now the length of the array can be odd or even. 
Median of an array | The Coding Shala
let's solve the median of two sorted arrays.

Method 1:
We have two sorted arrays, now if we merge both arrays into one(still sorted) then we can easily find the center of the merged array, But this method takes O(n+m) time and O(n+m) extra space. here n and m are lengths of given arrays. This is a simple approach to solve this problem. Let's code it first using this method then we will solve it in a log(m+n) time.

Java Code: 

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        double ans = 0;
        int len1 = nums1.length;
        int len2 = nums2.length;
        int[] arr = new int[len1+len2];
        int i=0, j=0,k=0;
        while(i<len1 && j<len2){
            if(nums1[i]<=nums2[j]){
                arr[k] = nums1[i];
                i++;
                k++;
            }else{
                arr[k] = nums2[j];
                k++;
                j++;
            }
        }
        while(i<len1){
            arr[k] = nums1[i];
            i++;
            k++;
        }
        while(j<len2){
            arr[k] = nums2[j];
            j++;
            k++;
        }
        int len = arr.length;
        if(len%2 != 0) ans = (double)arr[len/2];
        else{
            ans = (double)(arr[(len-1)/2] + arr[(len/2)])/2;
        }
        return ans;
    }
}

Method 2: 
Time Complexity: O(log(m+n)).
Space Complexity: O(1).

The median is used for dividing a set into two equals subsets that one subset is always greater than the others.

Now let's take an example of how to solve this problem in log(m+n) time.

We have two sorted arrays A and B.
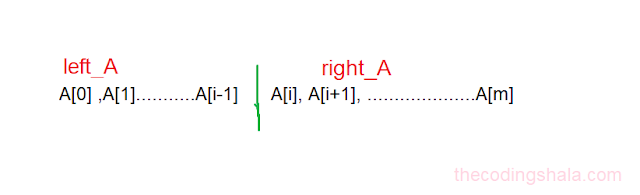
First, let's cut array A[] into two parts at a random position i.
Median of Two Sorted Arrays - The Coding Shala
Here, the size of A[] is m so we can make m+1 cuts(i=0 to m). When i=0 left_A is empty and when i=m, right_A is empty.
Now the same way we cut B[] into two parts at a random position j.
Median of Two Sorted Arrays - The Coding Shala
As a next step, we will put left_A and left_B into one set and put right_A and right_B into another set.
Median of Two Sorted Arrays - The Coding Shala
When we find such a cut where

                      A[i-1] <= B[ j ] and,
                      B[ j-1 ] <= A[i]

and exactly we need to find this condition. We will return the median of two sorted arrays using these four elements.

The median is: 
Median of Two Sorted Arrays - The Coding Shala
We will use a binary search to find these cuts(partitions). 
Note: take m<n.

How will we make these cuts(partitions)? Take two variables min_index and max_index and initialize min_index to 0 and max_index to m(length of the smaller array).

To Partition A[], use formula (min_index + max_index)/2 and insert it to i(mid for A[]).

To partition B[], use the formula (n+m+1)/2 - i and insert in to a variable j(mid for B[]).

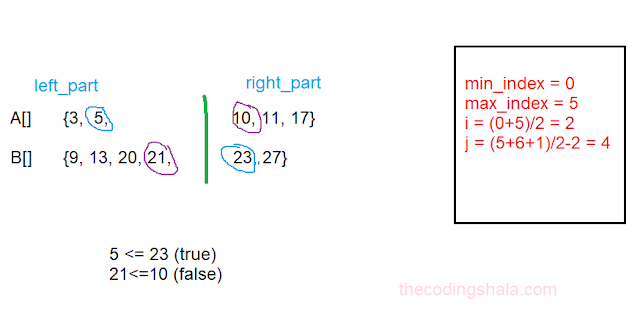
Now, let's take an example first to understand this approach:

we have two arrays: 
                               A[] = {3,5,10,11,17}
                               B[] = {9, 13, 20, 21, 23, 27}
After the first iteration:
Median of Two Sorted Arrays Example - The Coding Shala
here, condition is not satisfies so move forward and set min_index to i+1.

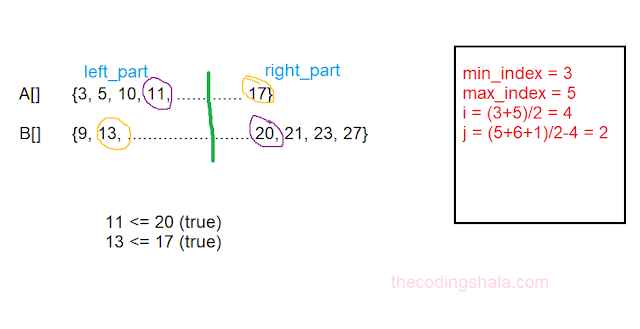
second iteration:
Median of Two Sorted Arrays Example - The Coding Shala
here, condition is satisfied so (n+m) = (5+6) is 11 is odd length, median is max(11,13) is 13.

Now let's code it.

Java Code: 

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        
        //take smaller array first
        if(m>n) return findMedianSortedArrays(nums2, nums1);
        
        int i=0,j=0; //for mid point 
        int min_index = 0;
        int max_index = m;
        int half = (m+n+1)/2;
        //binary search
        while(min_index <= max_index){
            //mid for first array
            i = (min_index+max_index)/2;
            //mid for second array
            j = half-i;
            
            //move min_index to mid+1
            if(i<m && j>0 && (nums1[i]<nums2[j-1])) min_index = i+1;
            //move max_index to mid-1
            else if(i>0 && j<n && (nums1[i-1]>nums2[j])) max_index = i-1;
            else{
                //here our condition matched
                //nums1[i-1]<=nums2[j]
                //and
                //nums2[j-1]<=nums1[i]
                break;
            }
        }
        
        //find out max of left half
        int max_left = 0;
        if(i==0) max_left = nums2[j-1];
        else if(j==0) max_left = nums1[i-1];
        else{
            max_left = Math.max(nums1[i-1], nums2[j-1]);
        }
        
        if((m+n)%2 !=0){
            //median is max of first half
            //*1.0 for double
            return max_left*1.0;
        }
        
        //find min of right half
        int min_right = 0;
        if(i==m) min_right = nums2[j];
        else if(j==n) min_right = nums1[i];
        else{
            min_right = Math.min(nums1[i], nums2[j]);
        }
        //case 2 m+n is even length
        //median is avergae of max first half and min second half
        return (max_left+min_right)/2.0;
    }
}



Other Posts You May Like
Please leave a comment below if you like this post or found some error, it will help me to improve my content.
By

Comments

Post a Comment

Popular Posts from this Blog

Java Program to Convert Binary to Decimal - The Coding Shala

Home >> Java Programs >> Convert Binary to Decimal  Hey there, welcome back to another post. In this post, we will learn how to convert Binary to Decimal in Java. Java Program to Convert Binary to Decimal You have given a binary number, convert it to a decimal number. Example:  Input: 101 Output: 5 Input: 111 Output: 7 Binary to Decimal Conversion in Java Approach We will the below formula to convert binary to decimal: decimal number = (2^0) * (rightmost digit) + (2^1) * (second rightmost digit) + ...  for example:  binary number = 110 decimal number = 2^0 * 0 + 2^1 * 1 + 2^2 * 1 = 1 * 0 + 2 * 1 + 4 * 1 = 0 + 2 + 4 = 6 Java Program:  import java.util.Scanner; /** * https://www.thecodingshala.com/ */ public class Main { public static void printDecimal( int num) { int decimal = 0; int twos = 1; // 2^0 = 1 initial value while (num > 0) { ...
Read more

N-th Tribonacci Number Solution - The Coding Shala

Home >> Programming >> N-th Tribonacci Number  Hey there, welcome back to another post. In this post, we will learn how to solve the N-th Tribonacci Number problem and will implement its solution in Java. N-th Tribonacci Number Problem Statement The Tribonacci sequence Tn is defined as follows: T0 = 0, T1 = 1, T2 = 1, and Tn+3 = Tn + Tn+1 + Tn+2 for n >= 0. Given n, return the value of Tn.  Example 1:  Input: n = 4 Output: 4 Explanation: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4 N-th Tribonacci Number Java Solution using Bottom-Up DP This problem is similar to the Fibonacci series. We can solve it using the Bottom-Up approach of dynamic programming. Time Complexity: O(n) Space Complexity: O(n) The space complexity can be reduced to O(1) by using variables to store the previous three values instead of using an array. Java Program:  class Solution { public int tribonacci( int n) { if (n == 0) return 0; ...
Read more

Shell Script to Create a Simple Calculator - The Coding Shala

Home >> Scripting >> simple calculator Shell Script to Create a Simple Calculator Write a shell script to create a simple calculator using a switch-case statement? Code:  #! / bin / bash echo "simple calculator" sum = 0 i = "y" echo "enter first number" read n1 echo "enter second number" read n2 while [ $ i = "y" ] do echo "1.Addition" echo "2.Subtraction" echo "3.Multiplication" echo "4.Division" echo "Enter choice" read ch case $ch in 1 ) sum =$(echo " $n1 + $n2" | bc - l) echo "Addition is =" $ sum ;; 2 ) sum =$(echo "$n1 - $n2" | bc - l) echo "Sub is =" $ sum ;; 3 ) sum =$(echo "$n1 * $n2" | bc - l) echo "Mul is =" $ sum ;; 4 ) sum =$(echo "$n1 / $n2" | bc - l) echo "div is =" $ sum ;; * )echo "invalid choice" esac echo "Do y...
Read more

LeetCode - Shuffle the Array Solution - The Coding Shala

Home >> LeetCode >> Shuffle the Array  In this post, we will learn how to solve LeetCode's Shuffle the Array problem and will implement its solution in Java. Shuffle the Array Given the array nums consisting of 2n elements in the form [x1,x2,...,xn,y1,y2,...,yn]. Return the array in the form [x1,y1,x2,y2,...,xn,yn]. Example 1: Input: nums = [2,5,1,3,4,7], n = 3 Output: [2,3,5,4,1,7]  Explanation: Since x1=2, x2=5, x3=1, y1=3, y2=4, y3=7 then the answer is [2,3,5,4,1,7]. Example 2: Input: nums = [1,2,3,4,4,3,2,1], n = 4 Output: [1,4,2,3,3,2,4,1] Practice this problem on LeetCode: Click Here. Shuffle the Array Java Solution Approach 1: Using a new Array. Space complexity: O(n). Java Program:  class Solution { public int [] shuffle ( int [] nums , int n ) { int [] ans = new int [ 2 * n ]; int j = 0 ; for ( int i = 0 ; i < 2 * n ; i = i + 2 ){ ans [ i ] = nums [ j ]; ans...
Read more

Java Program to Find GCD or HCF of Two Numbers - The Coding Shala

Home >> Java Programs >> Find GCD of Two Numbers  Hey there, welcome back to another post. In this post, we will learn how to find GCD or HCF of Two Numbers in Java. Java Program to Find GCD or HCF of Two Numbers The GCD (Greatest Common Divisor) or HCF (Highest Common Factor) of two numbers is the largest number that divides both of them. For example:  Number1: 6 (2 * 3) Number2: 9 (3 * 3) GCD or HCF of 6 and 9 is: 3 Find GCD of Two Numbers in Java using for Loop As we already know, GCD is the largest number that divides both numbers. We can start a for loop from 1 (because 1 divides all the numbers) to both numbers and if it divides both numbers then update GCD. Java Program:  import java.util.Scanner; /** * https://www.thecodingshala.com/ */ public class Main { public static void findGCD( int num1, int num2) { int gcd = 1; if (num1 == 0) { gcd = num2; } if (num2 == 0) { ...
Read more