Introduction to Graph Data Structure - The Coding Shala
Home >> Data Structures >> Introduction to Graph
Other Posts You May Like
Please leave a comment below if you like this post or found some error, it will help me to improve my content.
Introduction to Graph Data Structure
The graph is one of the most important data structures that solve many real-world problems. A graph is a non-linear data structure. A Graph organizes items in an interconnected network. The following is an example of the graph:
A graph G is an ordered pair of a set V of Vertices and a set E of Edges.
G = (V,E).
Ordered pair means: (a,b) not equals to (b,a) if, a not equals to b.
Unordered pair is: {a,b} = {b,a}
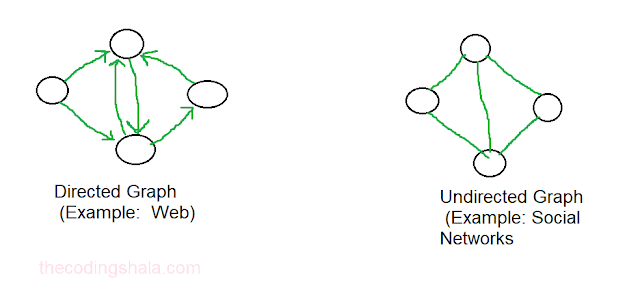
In the graph, edges can be two types: Directed and Undirected edges.
So based on the edges type graph can be two types:
G = (V,E).
Ordered pair means: (a,b) not equals to (b,a) if, a not equals to b.
Unordered pair is: {a,b} = {b,a}
In the graph, edges can be two types: Directed and Undirected edges.
- A directed graph or Digraph
- An undirected graph
In the directed graph there is a direction from one vertex to another. An example of a Directed graph is the Internet(Web). In Web one page contains a link to another page but the reverse is not necessary.
In the undirected graph, edges are bidirectional. An example of an undirected graph is a social network like Facebook.
Weighted and Unweighted Graph
A graph can be weighted or unweighted. Weighted graph means each edge contains some weight(value). In an unweighted graph, edges do not contain any values they all are having the same weight(1).
Properties of Graph
The following are some properties of a graph:
Self Loop: An edge from a node to itself.
Multi-edge: If There is more than one edge between two vertices then its called multi-edges.
If a graph does not contain self-loop and multi-edge called a simple graph.
How to find the number of edges in a simple graph?
In a graph, if the number of vertices is |v| = n
then, edges are
0 <= |E| <= n*(n-1) , if graph is directed.
0 <= |E| <= (n*(n-1))/2 ,if graph is undirected.
Dense Graph: If a graph contains too many edges almost near to the maximum number of edges called a dense graph.
Sparse Graph: If a graph contains few edges almost equal to the number of vertices called sparse graph.
Path: A sequence of vertices where each adjacent pair is connected by an edge is called path is also known as a Walk.
Simple Path: A path in which no vertices and edges are repeated call simple path.
Trail: A Trail is a walk in which no edges are repeated.
Strongly connected graph: In a graph, if there is a path from any vertex to any other vertex then the graph is called a strongly connected graph. If a graph is undirected then we simply called it a connected graph.
Cyclic or Acyclic Graph: If a graph contains a cycle called Cyclic graph otherwise Acyclic graph.
Graph Coloring: If we assign colors to each node in a graph called graph coloring. A legal coloring is if no adjacent nodes have the same color.
Graph Representations
The most commonly used representation of a graph are:
- Adjacency Matrix
- Adjacency List
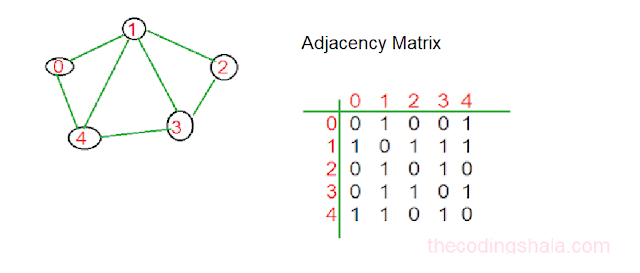
Let's take an example
Adjacency Matrix
We take a 2D array of size V*V, where V is the number of vertices in a graph and array[i][j]=1 indicates that there is an edge. Adjacency Matrix for the above example graph is:
Adjacency List
We used an array of lists. The size of the array is the number of vertices and arr[i] represents the list of vertices adjacent to the ith vertex. The following is the adjacency list representation of the above graph:
Generally, we used the adjacency list for sparse graph and adjacency matrix for dense graphs.
Graph Traversals
There are 2 popular approaches to doing graph traversals is:
- Depth-First Search(DFS)
- Breadth-First Search(BFS)
That's it for the introduction of graphs. We will see all the topics in detail in coming posts.
Other Posts You May Like
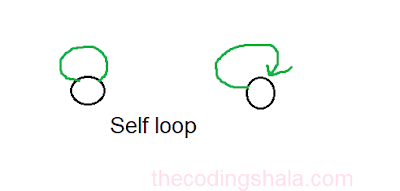
Comments
Post a Comment